1. Find the values of all six trigonometric functions for the given angle 225 deg

Solution:
`theta=225` (deg)

`theta=225^circ`

We know that `225^circ=180^circ+45^circ`

Reference angle `=45^circ`

A 45-45-90 triangle is an isosceles right triangle, where the both legs are equal say `1` and the hypotenuse is `sqrt{2}`

`x=1,y=1,r=sqrt{2}`


`225^circ` is in Quadrant-3 and here x is -ve and y is -ve


So, `x=-1,y=-1,r=sqrt(2)`


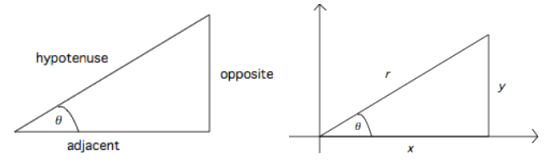
Opposite side `(y)`, adjacent side `(x)` and hypotenuse `(r)`

`sin(theta), cos(theta), tan(theta)` fromula

`sin(theta) = "opposite"/"hypotenuse" = y/r`

`cos(theta) = "adjacent"/"hypotenuse" = x/r`

`tan(theta) = "opposite"/"adjacent" = y/x`

`csc(theta) = "hypotenuse"/"opposite" = r/y`

`sec(theta) = "hypotenuse"/"adjacent" = r/x`

`cot(theta) = "adjacent"/"opposite" = x/y`

`(1)` `sin(theta)=y/r=(-1)/(sqrt(2))=(-sqrt(2))/2=-0.7071`

`(2)` `cos(theta)=x/r=(-1)/(sqrt(2))=(-sqrt(2))/2=-0.7071`

`(3)` `tan(theta)=y/x=(-1)/(-1)=1`

`(4)` `csc(theta)=r/y=(sqrt(2))/(-1)=-sqrt(2)=-1.4142`

`(5)` `sec(theta)=r/x=(sqrt(2))/(-1)=-sqrt(2)=-1.4142`

`(6)` `cot(theta)=x/y=(-1)/(-1)=1`