|
|
|
|
Home > Geometry calculators
|
|
|
Educational Level
|
Secondary school, High school and College |
|
Program Purpose
|
Provide step by step solutions of your problems using online calculators (online solvers)
|
|
Problem Source
|
Your textbook, etc |
|
|
1. Coordinate Geometry
2. Graphs
1. Graphs - Plotting of mathematical functions f(x) or f(y)
2. Graph - Using Points and Slope
2.1 Points : (3,-5),(5,3)
2.2 Points on X-axis : -3,5,12,-7,0
2.3 Points on Y-axis : -3,5,12,-7,0
2.4 Lines : x=-3y+5; 2x+y=1; x+2y<=5; x+y>=15
2.5 Line using Slope & point : Slope=7 and Point=(4,6)
2.6 Line using Slope & Y-Intercept : Slope=2 and Y-Intercept=-4
2.7 Line passing through two points : Point1=(3,-5) and Point2=(5,3)
3. Circle
4. Ellipse
5. Parabola
6. Hyperbola
7. Polar Graph
3. Area
1. Area of a Circle
2. Area of a Semi-Circle
3. Area of a Regular Hexagon
4. Area of a Square
5. Area of a Rectangle
6. Area of a Parallelogram
7. Area of a Rhombus
8. Area of a Trapezium
9. Area of a Scalene Triangle
10. Area of a Rightangle Triangle
11. Area of a Equilateral Triangle
12. Area of a Isosceles Triangle
13. Area of a Sector Segment
4. Volume
1. Volume of a Cuboid
2. Volume of a Cube
3. Volume of a Cylinder
4. Volume of a Cone
5. Volume of a Sphere
6. Volume of a Hemi-Sphere
Radius of Circle, Diameter of Circle, Circumference of Circle, Perimeter of Circle, Area of Circle,
Radius of Semi-Circle, Diameter of Semi-Circle, Circumference of Semi-Circle, Perimeter of Semi-Circle, Area of Semi-Circle,
Side of RegularHexagon, Perimeter of RegularHexagon, Area of RegularHexagon,
Side(a) of Square, Diagonal of Square, Perimeter of Square, Area of Square,
Length of Rectangle, Breadth of Rectangle, Diagonal of Rectangle, Perimeter of Rectangle, Area of a Rectangle,
Perimeter of Parallelogram, Area of Parallelogram,
Perimeter of Rhombus, Area of Rhombus,
Perimeter of Trapezium, Area of Trapezium,
Perimeter of Scalene Triangle, Area of Scalene Triangle,
BC of Rightangle Triangle, AC of Rightangle Triangle, Perimeter of Rightangle Triangle, Area of Rightangle Triangle,
Side of Equilateral Triangle, Perimeter of Equilateral Triangle, Area of Equilateral Triangle,
b of Isoceles Triangle, h of Isoceles Triangle, Perimeter of Isoceles Triangle, Area of Isoceles Triangle,
Radius of SectorSegment, angle of measure of SectorSegment, length of arc of SectorSegment, area of minor sector of SectorSegment,
Diagonal of Cuboid, Curved Surface Area of Cuboid, Total Surface Area of Cuboid, Volume of Cuboid,
Diagonal of Cube, Curved Surface Area of Cube, Total Surface Area of Cube, Volume of Cube,
Curved Surface Area of Cylinder, Total Surface Area of Cylinder, Volume of Cylinder,
Slant Height(l) of Cone, Height(h) of Cone, Curved Surface Area of Cone, Total Surface Area of Cone, Volume of Cone,
Radius of Sphere, Diameter of Sphere, Curved Surface Area of Sphere, Total Surface Area of Sphere, Volume of Sphere,
Radius of Hemi-Sphere, Diameter of Hemi-Sphere, Curved Surface Area of Hemi-Sphere, Total Surface Area of Hemi-Sphere, Volume of Hemi-Sphere,
5. Pythagorean Theorem
|
|
1.
General Graph
|
1. `y = x`
2. `y <= sin(x)`
3. `y >= cos(x)`
4. `y = sqrt(x)`
5. `y <= sqrt(x^3-3x)`
6. `y >= |x|`
7. `y = x^3-x`
8. `y <= (e^x-e^(-x))/2`
1. `x = sin(y)`
2. `x <= cos(y)`
3. `x >= sqrt(y)`
4. `x = sqrt(y^3-3y)`
5. `x <= |y|`
6. `x >= sin(y)^3+cos(y)^3`
7. `x = y+sin(y)`
8. `x <= (sin(9y)+sin(10y))*sin(0.1y)`
|
|
|
2.
Graph - Using Points and Slope
|
1. Points
like (3,-5),(5,3)
2. Points on X-axis
like -3,5,12,-7,0
3. Points on Y-axis
like -3,5,12,-7,0
4. Lines
like x=-3y+5; 2x+y=1; x+2y<=5; x+y>=15
5. Line using Slope & point
like Slope=7 and Point=(4,6)
6. Line using Slope & Y-Intercept
like Slope=2 and Y-Intercept=-4
7. Line passing through two points
like Point1=(3,-5) and Point2=(5,3)
|
|
|
|
|
3.
Circle
|
1. Circle-1
`X^2 + Y^2 = 9`
2. Circle-2
`(X+1)^2 + Y^2 = 12`
3. Circle-3
`X^2 + (Y-2)^2 = 15`
4. Circle-4
`(X+1)^2 + (Y-2)^2 = 9`
|
|
|
4.
Ellipse
|
1. Ellipse-1
`X^2/4 + Y^2/9 = 9`
2. Ellipse-2
`(X+1)^2/4 + Y^2/9 = 12`
3. Ellipse-3
`X^2/4 + (Y-2)^2/9 = 15`
4. Ellipse-4
`(X+1)^2/4 + (Y-2)^2/9 = 9`
|
|
|
|
|
5.
Parabola
|
1. Parabola-1
`Y = 3X^2`
2. Parabola-2
`Y = 3X^2 + 1`
3. Parabola-3
`Y = 3(X+1)^2`
4. Parabola-4
`Y = 3(X+1)^2 + 1`
5. Parabola-5
`X = 3Y^2`
6. Parabola-6
`X = 3Y^2 + 1`
7. Parabola-7
`X = 3(Y+1)^2`
8. Parabola-8
`X = 3(Y+1)^2 + 1`
|
|
|
6.
Hyperbola
|
1. Hyperbola-1
`X^2/4 - Y^2/9 = 9`
2. Hyperbola-2
`2. (X+1)^2/4 - Y^2/9 = 12`
3. Hyperbola-3
`X^2/4 - (Y-2)^2/9 = 15`
4. Hyperbola-4
`(X+1)^2/4 - (Y-2)^2/9 = 9`
5. Hyperbola-5
`Y^2/4 - X^2/9 = 9`
6. Hyperbola-6
`(Y+1)^2/4 - X^2/9 = 12`
7. Hyperbola-7
`Y^2/4 - (X-2)^2/9 = 15`
8. Hyperbola-8
`(Y+1)^2/4 - (X-2)^2/9 = 9`
|
|
|
|
|
7.
Polar Graph
|
1. `R = 4*cos(2*t)`
2. `R = 4*sin(2*t)`
3. `R = 2-4*sin(2*t)`
4. `R = 2-4*cos(2*t)`
5. `R = 2+4*cos(2*t)`
6. `R = 2+4*sin(2*t)`
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.
Rhombus
|
Radius `(r_1) = (d_1)/2`
Radius `(r_2) = (d_2)/2`
Side `(a) = sqrt(r_1^2 + r_2^2)`
Perimeter `(P) = 4 a`
Area `(SA) = (d_1 d_2)/2`
I know that for a rhombus d1 = 10 and d2 = 24 . From this find out Area of the rhombus.
`"Here, we have " d_1 = 10" and " d_2 = 24" (Given)"`
`a^2 = (d_1/2)^2 + (d_2/2)^2`
`a^2 = (10/2)^2 + (24/2)^2`
`a^2 = (5)^2 + (12)^2`
`a^2 = 169`
`a = 13`
`"Perimeter" = 4 * a`
` = 4 * 13`
` = 52`
`"Area" = 1/2 " (Product of diagonals)"`
` = 1/2 * d_1 * d_2`
` = 1/2 * 10 * 24`
` = 120`
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.
Cuboid
|
Diagonal `(d) = sqrt(l^2+ b^2+ h^2)`
Surface Area `(SA) = 2 (lb + bh + hl)`
Volume `(V) = lbh`
I know that for a cuboid Length = 3 , Breadth = 4 , and Height = 5 . From this find out Volume of the cuboid.
`"Here, we have " l = 3, b=4, h=5" (Given)"`
`"Diagonal"^2 = l^2 + b^2 + h^2`
`"Diagonal"^2 = 3^2 + 4^2 + 5^2`
`"Diagonal"^2 = 50`
`Diagonal = 7.0711`
`"Here, we have " l = 3, b=4, h=5" (Given)"`
`"Volume" = l * b * h`
` = 3 * 4 * 5`
` = 60`
`"Here, we have " l = 3, b=4, h=5" (Given)"`
`"Total Surface Area" = 2 (lb + bh + lh)`
` = 2 * (3 * 4 + 4 * 5 + 3 * 5)`
` = 2 * (47)`
` = 94`
`"Here, we have " l = 3, b=4, h=5" (Given)"`
`"Curved Surface Area" = 2h (l + b)`
` = 2 * 5 (3 + 4)`
` = 70`
|
|
|
2.
Cube
|
diameter `(d) = sqrt(2) l`
Diagonal `= sqrt(3) l`
Surface Area `(SA) = 6 l^2`
Volume `(V) = l^3`
I know that for a cube Length = 3 . From this find out Volume of the cube.
`"Here, we have " l = 3`
`"Diagonal" = sqrt(3) l`
` = sqrt(3) * 3`
` = 5.1962`
`"Here, we have " l = 3`
`"Volume" = l^3`
` = 3^3`
` = 27`
`"Here, we have " l = 3`
`"Total Surface Area" = 6 l^2`
` = 6 * 3^2`
` = 6 * 9`
` = 54`
`"Here, we have " l = 3`
`"Curved Surface Area" = 4 l^2`
` = 4 * 3^2`
` = 4 * 9`
` = 36`
|
|
|
|
|
|
|
4.
Cone
|
Height `(h) = sqrt(l^2 - r^2)`
Curved Surface Area `(CSA) = pi r l`
Total Surface Area `(TSA) = pi r (l + r)`
Volume `(V) = (pi r^2 h)/3`
I know that for a cone Radius = 3 and Length = 5 . From this find out Volume of the cone.
`"Here, we have Radius "(r) = 3" and Slant Height " (l) = 5" (Given)"`
`l^2 = r^2 + h^2`
`h^2 = l^2 - r^2`
`h^2 = 5^2 - 3^2`
`h^2 = 16`
`h = 4`
`"Volume" = (pi r^2 h)/3`
` = (pi * 3^2 * 4)/3`
` = 37.6991`
`"Total Surface Area" = pi r (l + r)`
` = pi * 3 (5 + 3)`
` = 75.3982`
`"Curved Surface Area" = pi r l`
` = pi * 3 * 5`
` = 47.1239`
|
|
|
|
|
|
|
|
|
Pythagorean Theorem
: In a right angled triangle, the square of the length of the hypotenuse
is equal to the sum of the squares of the lengths of the remaining sides.
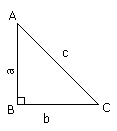
i.e. `AC^2 = AB^2 + BC^2`
Using Pythagoras
Theorem, Find out AC when AB = 5 and BC = 12
Here AB=5 and BC=12 (Given)
We know that,
In triangle ABC, by Pythagoras' theorem
`AC^2 = AB^2 + BC^2`
`AC^2 = 5^2 + 12^2`
`AC^2 = 25 + 144`
`AC^2 = 169`
`AC = 13`
|
|
|
|
Share this solution or page with your friends.
|
|
|
|
