2. The Equation for the terminal Side `theta` is `3x+5y=0` and `x>=0`. Find value of all six trigonometric functions Solution:`3x+5y=0`
`5y=-3x`
`y=-(3x)/5`
Here, `x>=0`
Let `x=5`
So `y=(-3)/5xx5=-3`
`P(5,-3)`
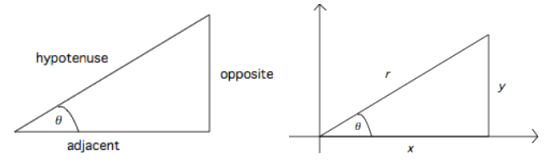
Opposite side `(y)`, adjacent side `(x)` and hypotenuse `(r)`
`sin(theta), cos(theta), tan(theta)` fromula
`sin(theta) = "opposite"/"hypotenuse" = y/r`
`cos(theta) = "adjacent"/"hypotenuse" = x/r`
`tan(theta) = "opposite"/"adjacent" = y/x`
`csc(theta) = "hypotenuse"/"opposite" = r/y`
`sec(theta) = "hypotenuse"/"adjacent" = r/x`
`cot(theta) = "adjacent"/"opposite" = x/y`
Here `x=5` and `y=-3`
In triangle ABC, by Pythagoras' theorem
`r^2 = x^2 + y^2`
`=5^2 + (-3)^2`
`=25 + 9`
`=34`
`:.r=sqrt(34)`
So, `x=5,y=-3 and r=sqrt(34)`
`(1)` `sin(theta)=y/r=(-3)/(sqrt(34))=(-3sqrt(34))/34=-0.5145`
`(2)` `cos(theta)=x/r=(5)/(sqrt(34))=(5sqrt(34))/34=0.85749`
`(3)` `tan(theta)=y/x=(-3)/(5)=-3/5`
`(4)` `csc(theta)=r/y=(sqrt(34))/(-3)=(-sqrt(34))/3=-1.94365`
`(5)` `sec(theta)=r/x=(sqrt(34))/(5)=1.16619`
`(6)` `cot(theta)=x/y=(5)/(-3)=(-5)/3=-5/3`
This material is intended as a summary. Use your textbook for detail explanation.
Any bug, improvement, feedback then
