3. Find the values of all six trigonometric functions for the given angle 330 deg

Solution:
`theta=330` (deg)

`theta=330^circ`

We know that `330^circ=360^circ-30^circ`

Reference angle `=30^circ`

A 30-60-90 triangle is a special right triangle, where the shortest leg (opposite `30^circ`) is `1`, the longer leg (opposite `60^circ`) is `sqrt{3}` and the hypotenuse (opposite `90^circ`) is `2`.

`x=1,y=sqrt(3),r=2`


`330^circ` is in Quadrant-4 and here x is +ve and y is -ve


So, `x=1,y=-sqrt(3),r=2`


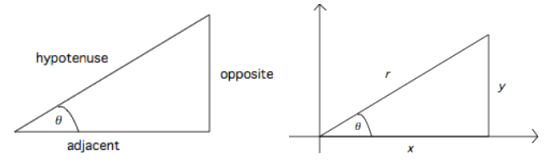
Opposite side `(y)`, adjacent side `(x)` and hypotenuse `(r)`

`sin(theta), cos(theta), tan(theta)` fromula

`sin(theta) = "opposite"/"hypotenuse" = y/r`

`cos(theta) = "adjacent"/"hypotenuse" = x/r`

`tan(theta) = "opposite"/"adjacent" = y/x`

`csc(theta) = "hypotenuse"/"opposite" = r/y`

`sec(theta) = "hypotenuse"/"adjacent" = r/x`

`cot(theta) = "adjacent"/"opposite" = x/y`

`(1)` `sin(theta)=y/r=(-sqrt(3))/(2)=-0.866`

`(2)` `cos(theta)=x/r=(1)/(2)=1/2`

`(3)` `tan(theta)=y/x=(-sqrt(3))/(1)=-sqrt(3)=-1.7321`

`(4)` `csc(theta)=r/y=(2)/(-sqrt(3))=(-2)/(sqrt(3))=(-2sqrt(3))/3=-1.1547`

`(5)` `sec(theta)=r/x=(2)/(1)=2`

`(6)` `cot(theta)=x/y=(1)/(-sqrt(3))=(-1)/(sqrt(3))=(-sqrt(3))/3=-0.5774`

---

---